Risk Assessment
Here we assess the risk of de-orbit system concepts disabling operational satellites or creating large orbit debris.
When a small object (impactor, or projectile) strikes a large object (target), there is sufficient kinetic energy in the impactor due to the very high closing speed (typically around 10 km/s) that the impactor typically will be completely vaporized. If the kinetic energy of the impactor in relation to the mass of the target is sufficiently large, then the target will usually suffer complete disruption and will break up into many fragments including many dangerous new debris objects with sizes larger than 10 cm. Naturally, the exact amount of fragmentation depends on where the impactor strikes the target in relation to its major elements, but in general, there is a threshold value of energy (of impactor) to mass (of target) beyond which complete fragmentation can be assumed to occur. This ratio is called EMR (energy-to-mass ratio). The specific threshold value of EMR is not discussed here due to ITAR concerns. If the EMR is well below this threshold value, then local damage will occur near the impact site, but complete disruption of the target is very unlikely.
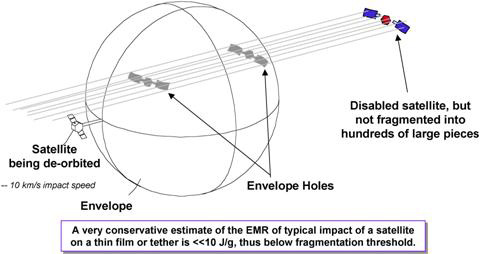
If a satellite-sized object weighing 1200 kg and having a 4.0 m2 cross-section area (CSA) were to collide with a very thin film, the area of the film of the cross-section area of the object would, in essence, “impact” the object. If the film were 6.35 micron thick Kapton (areal density of 9 g/m2), the total “projectile” mass is about 36 grams spread out over the entire CSA. Assuming a projectile speed of 10 km/s, the kinetic energy of this projectile is 1.8x106 J. Since the target object has a mass of 1.2x106 g (or 1200 kg), the energy-to-mass ratio or EMR (i.e. the energy per unit mass deposited into an object) is 1.5 J/g, well below the accepted threshold for breakup or disruption. For a normal impact with an enclosed envelope there are actually two impacts with the film. For impacts with very thin films or a deployed enclosed envelope constructed of a very thin film, catastrophic fragmentation and breakup of an object will not likely occur, as depicted in the figure below. However, for impacts with much thicker rigidized films or booms these are expected to cause disruption of the target. Despite the low EMR of the collision between a thin film and a spacecraft, appendages with low areal density, such as solar panels, will receive sufficient momentum during the collision that they will move significantly with respect to the main body and their attachment structure could be deformed permanently or even broken. This unlikely event may disable an operational spacecraft, but will not create a large number of new debris fragments.
An analysis has been carried out that estimated the effective collision cross-section (ATP) for various de-orbit systems for two important impact scenarios. These impact scenarios are 1) low-energy collisions that can disable other satellites and 2) high-energy collisions that can generate large new debris objects. The table below compares the effective collision cross-sectional ATP for several methods of de-orbiting space hardware following end of mission. In the “High-energy Collisions” column, the ATP is computed for collisions between portions of the de-orbiting system and debris objects with a typical dimension of 2 m. High-energy collisions are those collisions that generate many new large debris objects (greater than 10 cm in size). Low-energy collisions are those collisions that do not generate a significant number of new large debris objects. In all cases, the example spacecraft is similar to the reference used earlier – a 1200-kg spacecraft with cross-section area of 4.0 m2 starting at an altitude of 830 km (a typical polar sun-synchronous orbit). However, this pure drag area is augmented depending on the size of orbit debris. Here we are using a debris object size of 2.0 m because most of the area of orbital debris is concentrated in . In addition, this size is a conservative assumption for characteristic size for operating satellites, which, in many cases, can be much larger.
A bare spacecraft takes several centuries to de-orbit, and all its collisions are high-energy because all collisions are with the hard body (spacecraft). There are no extended thin areas. Thus the entry in the low-energy collisions column is zero.
The propulsive de-orbit assumes complete immediate de-orbit using propulsion. The time from the assumed delta-velocity is on the order of an hour, so the integrated area time product is negligible in terms of m2-years. This approach obviously poses the lowest risk of collision with debris, but is expensive mass-wise and cost-wise.
The inflation-maintained ultra-thin envelope (i.e. GOLD) reduced the time to de-orbit from centuries to months, and the only high-energy portion of the area is the hard body spacecraft. Thus, the associated ATP is quite low. Almost all of the area is the very thin film, which does not produce large new debris upon impact, so the ATP is the large value shown in the low energy collision column. This value is still very much lower than for the original bare spacecraft due to the different collision cross-section area augmentation.
For the rigidizable space inflatable sphere, the areal density is assumed to be high enough (100-200 g/m2) that all collisions will produce many new large debris fragments. Thus all the ATP is in the high-energy collisions column. The value is the same as for the previous row because the same area is used in both calculations.
For the boom-supported film, we have assumed the same projected drag area, but the area associated with the booms (their length multiplied by the assumed 2 m dimension of the debris) added to the bare spacecraft area (augmented by collision with 2-m debris) is used in computing the high-energy collision ATP. The thin film between booms contributes only to low-energy collisions and makes up the bulk of the collision ATP.
For both the gravity gradient tape and the electrodynamic tether, a dense tip mass of essentially zero size is assumed at the end of the tether or tape away from the spacecraft. This tip mass is needed to allow sufficient gravity gradient torque to prevent the tether or tape from swinging backwards and upwards due to the very force they are using to de-orbit the system. The collision cross-sectional area of this tip mass is equal to the area of the colliding debris object (i.e. 4m2). Thus the value in the high-energy collision column is a little larger than for the inflation-maintained ultra-thin envelope sphere. Both the tether and the tape have a very long vertical extent. This means that their low-energy collision cross-sectional area needs to be augmented by multiplying their length (5 and 3.3 km long, respectively) by the 2 m characteristic length of orbital debris and operational satellites. The N/A (not applicable) in the chart below under low-energy collisions for the bare spacecraft and rigidizable space inflatable is because all collisions are high-energy.
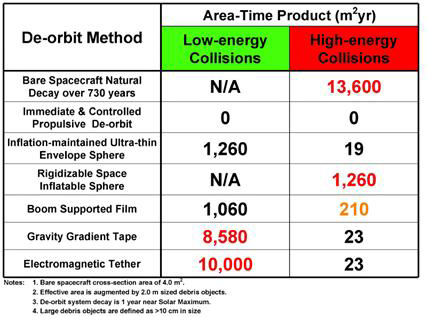
The greatest risk of high-energy collisions (that would create many new debris objects) occurs by leaving the satellite to decay naturally. Rigidizable Space Inflatable de-orbit systems pose the next highest risk since the envelope areal density is high enough to create large orbital debris objects or satellite disruption upon impact. Boom-supported films are the next most dangerous. Of the remaining concepts, electrodynamic tethers and gravity gradient tapes pose the greatest risk of low-energy collisions that could disable an operational spacecraft, but would not likely create many new debris fragments. Other than propulsive de-orbit, which requires more mass, the lowest threat is attributed to Inflation-maintained Ultra-thin Envelope type systems like GOLD.
We have learned that object or satellite disruption will not occur when the impact is with very thin films (~10 g/m2) or lightweight tethers (~3 g/m) since there is too little mass in the target, hence energy, to cause disruption. However, such an impact will likely disable an operating satellite. Boom Supported Film Aerobrakes, of which there are several different concepts, have a moderate risk of creating large debris objects due to the potential impact of large orbital debris objects or satellites with the rigid booms that are dense enough to cause object or satellite disruption.
|

